Wave Digital Filters in Reaktor

WHAT IS A WAVE DIGITAL FILTER?

Aside from having a somewhat cumbersome and awkward sounding name, Wave Digital Filters (WDFs) are also not necessarily filters, though they can be used for that purpose. They can serve a variety of other uses as well, including physical modelling and circuit simulation. This tutorial will focus upon circuit simulation.

In short, WDFs are made up of individual modules that represent components of a system. In the case of circuit simulation, this means resistors, capacitors, voltage sources, and inductors. Each element contains a wave input, a wave output, a value which determines port resistance, and a voltage value that measures the current over a given element. These basic building blocks are known as one port elements.

In addition to the elements that model electrical hardware, WDFs also contain adaptor elements, which can be used to connect the one port elements into more complex configurations. As far as I know, there are only two types of adaptor ports: parallel and serial. Adaptor elements will be covered more fully in the next tutorial.

For a more in-depth discussion of WDFs, there is a paper called Wave Digital Filters: Theory and Practice, by Alfred Fettweis which explains the motivation for and derivation of the math behind WDFs. Searching for this document online you may come across several sites (I’m looking at you, IEEE) attempting to charge exorbitant rates for a simple .pdf of a 25 year old paper! Don’t bother, here’s a free link.

CREATING ONE PORT ELEMENTS

One port elements are very simple modules. They are designed to attach to the adaptor elements – each adaptor can contain two elements (including other adaptors, which allows for very complex structures indeed). The elements contained within an adaptor are referred to as children, while the adaptor itself is called the parent.

So let’s take a look at designing one port elements. The following Reaktor structures are based upon code that can be found in Zolzer’s book in Chapter 12, written by a variety of well respected names in the academic DSP field.

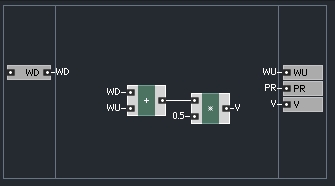
We can start by creating a somewhat generic macro that contains the pieces that are common to every one port element. We can define the wave in (called ‘wave down’ in WDF parlance), and the wave out (called ‘wave up’) simply by adding an input port called WD, and an output port called WU. The one port elements also contain an output named PR that gives the port resistance of the element to it’s parent adaptor.

Finally, each one port element has a function that can be used to calculate the voltage passing thru that element. This function is:

Voltage = 0.5*(WaveUp+WaveDown)

Putting all of these pieces together we get a generic macro that can be expanded upon to create one port elements that looks like this:

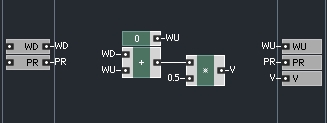
To turn a copy of this macro into a completed one port element, there are two more things we must add: a way to calculate port resistance, and a method to determine the wave out. Since a resistor is the simplest of one port elements, let’s start with that.

A resistor is measured in Ohms, as is the port resistance (PR) output. Hence we can simply create an input that describes the resistance of the element, and connect that value directly to the output to be sent to the parent adaptor.

Finally, the wave up output of a resistor is always equal to 0! For an explanation of this, please check Fettweis’ paper. However, if, like me, your background in electrical engineering is weak or non-existant, you may find it hard to follow.

Adding these changes to the generic macro shown above is simple:

This will suffice as a simple resistor model. Notice that since WU is always equal to zero, the WD + WU element can be removed. I left it in place for the sake of consistency.

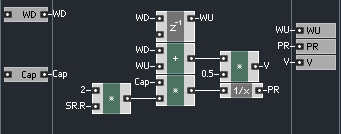
Now let’s define a model of a capacitor. First, let’s consider the port resistance. It would certainly be possible to simply have a PR input like the resistor model does, and to pass that to the output. However, capacitors are measured in Farads, not Ohms, so it would make more sense to take an input in Farads, and to translate that value into a port resistance value. The equation for this operation is:

R = 1/(2*C*Fs)

Where R is the port resistance, Fs is the sampling rate, and C is the value of capacitor in Farads.

To finish up our capacitor model, we need calculate the value of WU. This can be achieved using a simple unit delay, known in Core as the z^-1 module:

Next, let’s look at the build of an inductor model. Inductance is measured in Henrys, so again we must translate to a port resistance value:

R = 2*L*Fs

Where L is the inductance, and Fs is again the sampling rate. Implementing the wave up value of an inductor is a simple edit of the capacitor model, with the output being inverted like so:

The inductor model is not necessary for the tube diode we will build next time, however, it is a simple component to make so I included it for the sake of completeness.

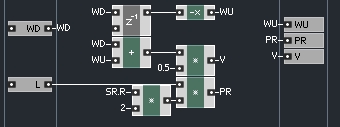
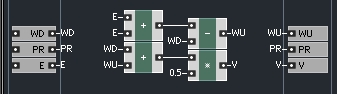
We have only a single one port element left to build – a voltage source. The voltage source has a resistance value that can be measured in Ohms, so we don’t need to worry about that, we can simply take a value provided by the user and pass it to the output of the macro.
Calculating the wave up value, however, is a little more interesting. The voltage source has an input that can be used to drive the WDF, called E. The wave up leaving the voltage source is equal to

WU = 2*E – WD

This leaves us with a simple macro that looks like this:

Notice that rather than multiplying E by 2, I simply added it to itself, which is mathematically identical, but saves a small piece of CPU by implementing an addition rather than a multiplication.

CONCLUSION

Okay! Now we have all of the one port elements we will need to build a simple tube diode model. In the next tutorial I will focus first upon the creation of a serial adaptor node that can be used to connect the one port elements together, then create our tube diode model.

All of the elements from today’s tutorial are fairly simple so I have not included a download. However a package of WDF elements will be made available with the next tutorial, so keep an eye out!

Please leave any feedback, questions or suggestions in the comments.