Oversampling in Reaktor, Part III

This tutorial is the third in a series on oversampling in Reaktor. In the previous tutorial, I showed a general structure that can be extended to create a polyphase filter with any number of taps and any (reasonable) amount of upsampling. This time, I’ll focus on getting ourselves back to the original sampling rate, using a similar but different structure.

DOWNSAMPLING POLYPHASE FILTER

In this section, I’ll create a generic macro that can be used for downsampling a signal. Like before, I will focus first and foremost upon making a macro that can be easily modularized and quickly modified to fit any type of oversampling system as needed.

Focusing on this means that the given macros for both up and downsampling are not nearly as efficient as they could be. For one, the efficiency can be increased substantially by replacing the table with constant values for each coefficient. Since the table is only being read from once, during initialization, I am at a loss to explain this difference except to blame the core compiler.

However, I am going to continue working today maintaining the table rather than using a Quick Constant for each coefficient. My reason for this is that I would like this framework to be as open-ended as possible, and allow the user to quickly create a new filter and modify it as necessary to fit their needs.

In sum, these structures are designed allow the user to change the number of taps and oversampling factor with the greatest amount of ease.

Once you have decided upon a final design for a filter, it might make sense to replace the table, however. On my machine I can save 1.5% of my CPU for a single voice, so this especially makes sense for polyphonic structures.

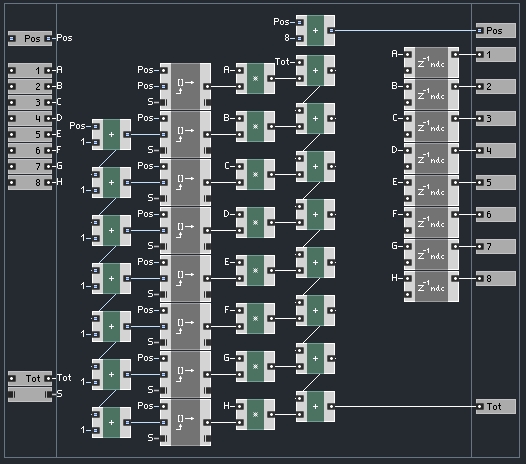
Now let’s get started on our downsampler. After splitting the incoming signal into several different waves, the downsampling filter must take each of those signals and combine them back into a single output. Since we already have an example of an 8x oversampler, let’s now downsample by 8 as well.

Each incoming signal essentially has it’s own FIR filter, the sums of which can be added up for the final output. Here’s macro that takes 8 inputs and implements a single tap for each one before passing them on to the output:

The ‘Tot’ value contains the running sum of all 8 filters.

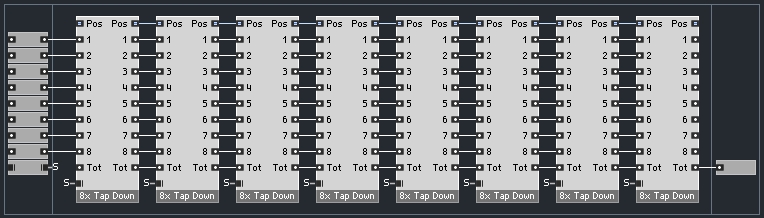
As with the upsampler structure introduced previously, this macro is designed to be strung together in multiple copies in a serial fashion like so:

Of course, the macro can easily be edited to have more or less sub-filters, so creating a polyphase filter with any oversampling factor you like should be pretty simple.

OVERSAMPLED WAVESHAPER

Using the simple waveshaper funtion

y = x / (|x| + 1)

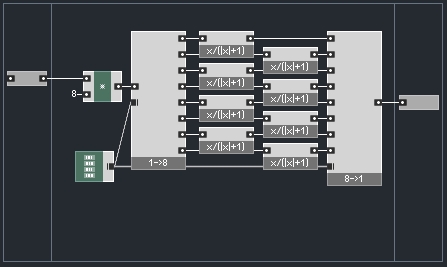
An oversampled waveshaper can be made like so:

Where the ‘1->8’ macro was introduced in the previous tutorial, and the ‘8->1’ macro is shown above.

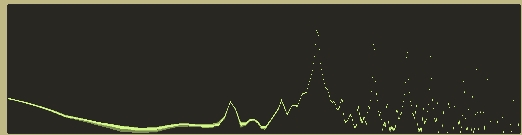
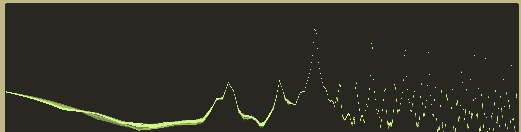
Here’s what the spectrum of this structure looks like with a high frequency Primary Sawtooth wave as an input (this is a test designed to cause bad aliasing, basically):

And here’s the same waveshaper, without oversampling:

While we are unable to completely remove the aliased signals, you can easily see a substantial reduction in aliasing across the spectrum in the top picture.

CONCLUSION

Over the last three tutorials, a system for rapidly designing and testing oversampling filters in Reaktor was introduced. I have included a download with this tutorial, which you can grab here.

It contains an ensemble for creating coefficients, and a few macros for quickly building polyphase filters. The ‘8x Tap Up’ macro can be used for 8x upsampling filters, while the ‘8x Tap Down’ is of course for downsampling. Both can easily be modified for different oversampling factors.

In the included ensemble, the filter coefficients are stored into an event table, which can be stored as a text file and loaded into a core table as demonstrated in the ‘8x Waveshaper’ macro.

I hope you have found this series useful, please feel free to ask for clarifications in the comments.