Building FX Part V - Filter Transfer Functions

In this tutorial I will show how to build a filter in Reaktor using nothing more than a mathematical description of a filter called a transfer function. Unfortunately, this requires a substantial amount of math. Fortunately, we can make do with just high school algebra so it’s not so bad. I’ll do my best to show each part of the process, and to provide links explaining any math we use.

TRANSFER FUNCTIONS

It is common to see filters described in terms of their transfer functions. Unfortunately, most texts assume that if you are reading about filters you understand what one is and what to do with it. Because of this, it took me quite a while to figure out how to use them properly.

Transfer functions are used to describe several types of systems. You can recognize a transfer function describing a digital filter because it will be in terms of H(z). In contrast, a transfer function describing an analog filter will commonly be in terms of H(s).

In this tutorial, I will present two typical transfer functions describing digital filters, and translate them, first into difference equations, which we will discuss more later, and finally, into Reaktor structures.

LOW PASS FILTER

Let’s start with a transfer function describing a very simple low pass filter:

In this equation, p is defined by user input, and can be any value between 0 and 0.98. It can mostly be ignored since when we implement the filter, it’s value will be supplied for us by a knob on the interface.

The first step on our quest to turn this into a filter is to re-write the equation in terms of X(z), the input of the filter, and Y(z), the output of the filter. This is very simple, we simply replace the H(z) term with Y(z)/X(z) like so:

This is interesting – if the term Y(z) refers to the output of the filter, all we have to do is solve for Y(z) (called a difference equation)and we can make the filter! To start, we can use the mathematical concept of cross multiplication to get rid of the fractions:

Finally, we can get rid of the negative exponents of z like so:

If Y(z) refers to the output of the filter, Y(z-1) refers to the output of the filter delayed by one sampling period.

To be honest, I’m not sure quite how this works, but it’s easy enough to implement: the value z^-1 was eliminated and the pY(z) became pY(z-1) instead . Each value of z with an exponent must be dealt with in this way (below, we’ll work on a more complex example that I think will make this process clear).

Now we are at a place where we can simply solve for Y(z) using basic algebra and implement the filter!

All I did here was add pY(z-1) to each side of the equation.

This final equation is what is referred to as a difference equation, we can use it to directly calculate the output, Y(z). A difference equation can be used to make a filter out of the current and previous values of X(z), and the previous values of Y(z).

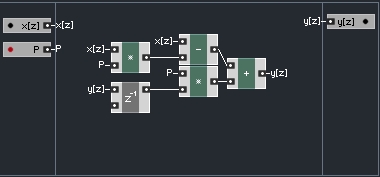
Okay, so Y(z) is the output of the filter, X(z) is the input, p is given to us by a knob, and Y(z-1) is the filter output delayed by a single sample. Using this information to make a filter in Reaktor is simple!

For this tutorial, I have chosen to use Reaktor Core to implement filters. I have several reasons for this – first, if you’re going to learn about filters in Reaktor and make them using this method, you should learn Core because it is better for this sort of stuff. Second, the y[z] signal would wrap backwards in Primary and look ugly, not to mention it’s harder to read that way. Third, I find the z^-1 module is a lot more descriptive of the math we are using than the Unit Delay, which it replaces.

PINK NOISE FILTER

For something a little more complicated, let’s make a pink noise filter as proposed by Robert Bristow-Johnson. A pink noise filter accepts white noise as input and ouputs pink noise. It basically works as a simple low pass filter with a static frequency response.

Okay then. Using the FOIL method, we can multiply out all of the values in this equation. I’m lazy, so I simply typed it into WolframAlpha, which gave me this response (check the expanded form section):

While I was at it, I also re-wrote the formula to be in terms of Y(z)/X(z), as in the first example.

Now we have a slight problem. We have a bunch of z values with positive exponents. For the purpose of making filters, we can only use negative exponents of z. Fortunately, this is an easy problem to solve – we can multiply both the top and the bottom of the equation by z^-a, where where a is the highest z exponent (also called the filter order, in this case, 3). So, after multiplying both parts of the fraction by z^-3, we get:

Remembering of course that z^0 is equal to 1!

As with the first example, our goal here is to solve for Y(z). And again, the best way to get there is to cross multiply terms:

Next, we multiply X(z) and Y(z) by their sides of the equation:

Once more, we eliminate the z  values by moving their exponents into the X(z) and Y(z) values:

Here, X(z-3), for example, refers to the input, delayed by 3 samples. Once again, to solve for Y(z), all we need to do is isolate it:

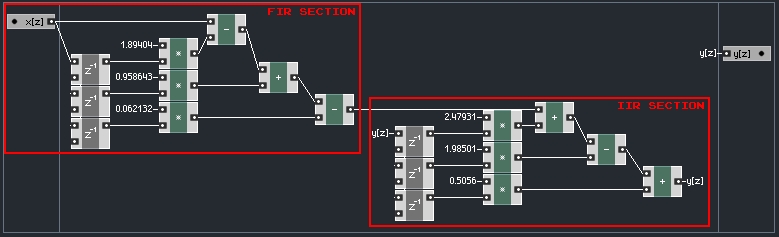
And done! Turning this into a Reaktor filter is a fairly simple task. Here’s what it looks like:

Each z^-1 module whose input is not immediately clear receives an input from the module directly above it.

CONCLUSION

Thanks for reading. It is my hope that you can use the information in this tutorial to find and build your own filters in Reaktor. If anything is unclear, please let me know in the comments and I’ll do my best to fix it.

If there is adequate interest, this series could continue by showing how to use a bilinear transform to convert an analog H(s) transfer function into a digital H(z) function. Please let me know if you are interested in this – if I receive no feedback I will assume there is no interest!