Bandwidth Limited Sawtooth Oscillator in Reaktor

This tutorial will focus on the creation of bandlimited oscillators in Reaktor, using the BLIT method (Bandwidth Limited Impulse Train). It builds off of subject matter previously introduced in two tutorials: Anti-Aliasing, Part I and Custom Core Oscillators, Part I. The reasons behind wanting a bandlimited oscillator, and the basic structure of an oscillator used in this tutorial are discussed in full in those two tutorials.

BANDWIDTH LIMITED IMPULSE TRAINS

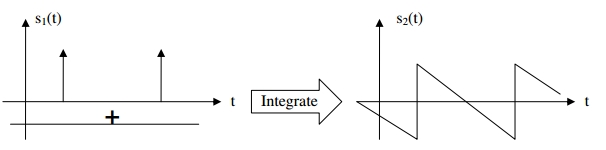
A basic solution to the creation of a basic ‘naive’ saw wave involves the integration of an impulse train added to a constant, negative signal. Here’s a visual representation:

I found this diagram to be confusing at first. So, on the left hand side of the diagram, there are two signals. On top is a signal that is equal to 0 most of the time but has two arrows pointing up. This signal is called an impulse train. The second signal on the left side is a constant, negative value.

At any point in time, these values are added together and then integrated. If you don’t know what integration is, it is a part of Calculus (don’t let that scare you off though). In DSP, integration is simple to achieve. To start, have a stored value (initialized to 0). When a new value arrives, you simply add the new value to the stored value. The sum becomes the new stored value. In fact, there is an integration module in Reaktor called the Integrator module.

So, the diagram works, as most of the time is it decreasing in value (since it is adding the sum of 0 and the negative value to it’s stored value each time). Every so often, the impulse train fires off, creating the immediate upward movement that gives us the sawtooth that we see on the right hand side of the diagram.

The sawtooth that results from this process will have significant aliasing artifacts. This stems from the fact that modelling an impulse train in a digital system like Reaktor is not very accurate. In reality, the impulse train should only be greater than 0 at a single instant. As short as a sampling period may be, it will still be infinitely longer than the theoretical ‘ideal’ impulse train.

For example, an ideal, analog impulse train might fire every second, on the second. It would be equal to 1 at that exact moment in time, and equal to 0 for the rest of the second. A digital representation of that analog signal would have the signal set to 1 for a single sample, and set to 0 for the rest. However, that single sample stretches a length of time substantially longer than the impulse from the analog signal. In short, creating a ‘naive’ digital impulse train causes aliasing.

Since this method causes aliasing, which is exactly the thing we are trying to avoid, why are we even talking about this?

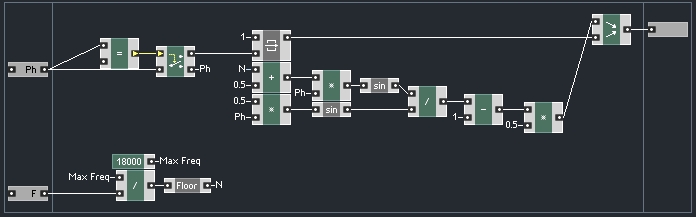
The answer is that we can use something very similar to this method to make a bandlimited sawtooth oscillator. To begin, we need to create a Bandwidth Limited Impulse Train (BLIT). The method I have had the most success with is called a DSF (Discrete Summation Formula) BLIT:

where θ is the incoming phase, and N is defined as

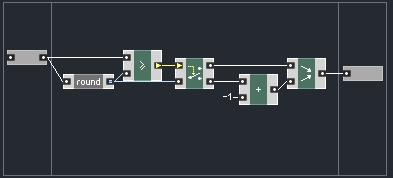
Floor is an operation that rounds down to the nearest integer that is less than the input.

The problem with this formula is that it has the potential to divide over 0 if the incoming phase is equal to 0. In reality, when the phase is equal to 0, we want the output to be 1. We can achieve this in Reaktor Core like so:

Floor is a module I created whose functionality is explained above. Inside, it looks like this:

If we use the phase accumulator from the previous tutorial, we can feed the BLIT macro with a phase from -π to π, and it will output an impulse train with a spectrum that looks like this:

As you can see, the amplitude drops to zero above 18000 Hz, the amount specified in the BLIT macro as “Max. Freq”. I should mention that you can use the Max. Freq. value as a sort of a low pass filter – the BLIT will not contain harmonics above the specified frequency, and neither will the sawtooth we make out of it. This is a pretty neat side effect of working with BLITs.

LEAKY INTEGRATOR

It would be nice if we could simply integrate the output of the BLIT macro and end up with a bandlimited sawtooth. Unfortunately, just like we need a special impulse train, we also will need a specialized integrator, known as a leaky integrator.

Leaky integrators are implemented as low pass filters (there may be other methods, but that is the one I am aware of). For more on filter design, check out the my tutorials on the subject (1, 2)

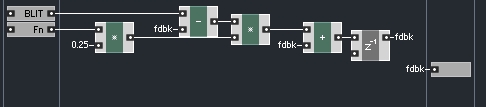
I have tried a few implementations of leaky integrators. Here is an implementation of a leaky integrator in core that I have to be work quite well:

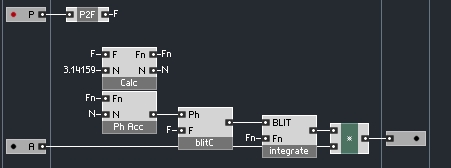
Put it all together and it looks like this:

This structure gives us a fully bandlimited sawtooth wave. Here’s the spectrum:

CONCLUSION

Now that we have a bandlimited sawtooth, it is not so much work to use the sawtooth to build bandlimited square and triangle waves as well. This will be the subject of the next tutorial in this series.

I have provided a sample oscillator from today’s tutorial here. It is saved as an Audio Core Cell.

As always, let me know in the comments if you have any questions or there is anything you would like to see covered in future installments.

* EDIT *

After posting this tutorial we had an email from ErrorSmith who said:

while checking it i noticed clicks during a pitch sweep when the last remaining harmonic becomes bigger than max freq and get muted.
Attached is a version that makes a smooth fade out for the harmonics during a sweep.
I compared you implementaion with the two others i found in the user lib. Yours is the most cpu friendly.

Here is his version of the file: Errorsmith Version