
Reaktor Tutorials
Implementing Math in Reaktor
Writing high-quality DSP code almost always requires a substantial amount of math. This leads many people to become frustrated – it’s hard to learn much of anything in the field without having long, confusing equations and terminology thrown at you.
If you are anything like me, you have a tendency to simply skip over any equations you see in a text. However, in DSP this will get you nowhere – in fact the math equations are often the most simple part of DSP papers to understand because they are not burdened by overcomplex terminology. In this tutorial, I’ll explain how I implement math in Reaktor, and how to look at equations with an eye towards understanding them.
DON’T BE INTIMIDATED!
I get a lot of questions about how I am capable of implementing this or that math function so easily. The simple answer of course, is that it only looks easy once it’s done and I understand it! However, I have a lot more to say on the subject.
Most of the math you encounter in early DSP is not any more complicated than what many people do in high school. Personally I dropped out of college after a year and half. I took a few somewhat advanced math classes in college, but that was 11 years ago now, and I took about 8 years off from doing math all together.
When I got into programming in Reaktor, I had to re-learn math that I knew when I was 16! I still have to look up concepts that I understood perfectly well in high school. Math is like that if you’re not always using it.
The number one rule in my book is not to be intimidated by anything! The first time I read Vadim Zavalishin’s tutorials on Zero Delay Feedback Filters, the very first sentence was gibberish to me, and it only went downhill from there. As you can read in this forum thread, I vowed to figure it out even if it took ‘6 months’. It took longer than that!
I spent months reading papers about all types of filters, slowly learning the terminology, and piecing together small parts of knowledge from forum posts and Wikipedia articles.
To do something like this, you need some skills, of course. Without some level of mathematical instruction in my life, this task would have been much harder. However, in my opinion, the most important component is to believe in yourself. There is no surer way to fail at something than to tell yourself you are incapable of doing it.
This means, the next time you see a huge equation with a ton of variables and confusing mathematical notation you don’t understand, don’t just tell yourself “Oh I can’t do that.” Instead, buckle down and try to figure it out! If you have to start at the bottom, like I did with filter design, this may require a lot of work on your part.
Of course, you should probably start with something small, that seems in the realm of possibility. Succeeding will bring you more confidence, more knowledge to build on, and more drive to learn and discover.
THE TWO THINGS YOU NEED TO KNOW
The nice thing about programming math is that you often don’t really need to actually *do* math – you just tell the computer to do it for you! Generally speaking, I like to think of math as two things that I need to know – the first is the order of operations, the second is notation. That’s it!
The order of operations is something that is (or should be, at least) taught to all math students in junior high. Simply put, it is a method of doing calculations in a particular order. While the concept is very simple, it can be complicated the by poor mnemonic devices used to teach children.
I understand there are some variations, but here in the United States, we use the phrase “Please Excuse My Dear Aunt Sally” (PEMDAS), which stands for Parantheses, Exponents, Multipy, Divide, Add, Subtract. Many people assume that therefore, addition happens before subtraction. It doesn’t. The real order of operation is:
1. Parantheses
2. Exponents
3. Multiplication and Division
4. Addition and Subtraction
A common error that many people will make (thinking addition comes before subtraction) is with something like the following question:
5-2+3 = ?
Sometimes, people will interpret this as:
5-(2+3) = 0
In reality, the answer is
5-2+3 = 6,
because 5-2 is 3 and 3+3 is 6. That is, addition and subtraction happen at the same time, from left to right.
Something more complex, like
5-2+3*6
will often get confused as well, by people who ignore the order of operations entirely, as meaning,
(5-2+3) * 6 = 36
These people are simply calculating all operators from left to right, another common mistake to avoid.
This should be interpreted as:
5-2+(3*6) = 21
since multiplication happens before addition and subtraction.
I hope this gives you a fair idea of how the order of operations works. If you ever want to check, WolframAlpha.com [LIIINKK] is a fantastic source for figuring this stuff out. Let’s say, for example, you had the equation
X – Y + Z
and you were unsure whether the addition or subtraction should happen first. You could choose arbitrary values for X, Y, and Z, and punch them into the search menu, and get a result something like this.
It then becomes very clear what the order is.
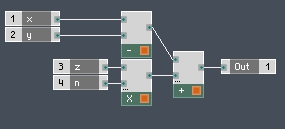
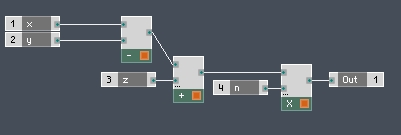
Once you understand which calculations need to be done first, you simply arrange your modules in that order. For example,
x-y+z*n,
the multiplication happens first, then you do the addition/subtraction from left to right. In Reaktor, you get:
Whereas, for the sake of comparison, the wrong way to do it the I discussed above (simply doing all equations from left to right) would look like this:
Okay, the second thing you need to know is notation. Unfortunately, this one is much more complicated, but only if you let it destroy your confidence will it prevent you from implementing an equation.
What I mean by notation is, simply looking at an equation and at least having an idea of what the symbols in that equation mean. This includes a few things.
First of all, variables. For example, if you see the term fs (where the s is really small, in subtext), you can be almost certain that this means the sampling rate, in Hertz (IE, 44100 or whatever your sampling frequency is). Likewise, an uppercase ‘T’ often refers to 1/fs.
I couldn’t possibly cover all of these – it would be disingenuous of me to pretend like I have a good grasp on them myself. Don’t despair, however, they will almost always be defined in the text.
The other part of notation is mathematical symbols. I’ll give an example of one that stopped me a few times when I got back into Reaktor. Now I don’t understand why I had such a block around it.
Okay, the Σ is a greek letter named sigma. When I first started encountering this a few years ago, I had the annoying realization that I had once known what this meant and understood it well, but I had no recollection of what it did anymore. For a long time I simply ignored anything that used it. Finally at some point, I decided to learn what Σ does, and it’s not that hard.
Simply put, the i = 0 at the bottom means that i starts at 0, and the 100 at the top means it ends at 100. Then, you calculate everything to the right of the Σ symbol, in this case you get the numbers
0, 0.5, 0.666, 0.75, 0.8, etc…
Then, you simply take all of the numbers aquired and add them together! That’s what Σ does, it sums an interated function. Let’s (finally) take a look at how you could solve the same sigma summation in Reaktor:
It’s not so hard!
Again, it’s impossible for me to cover all of mathematical notation (not that I even know it!), but the point is, this stuff isn’t that hard, you can figure it out. If there is a symbol you don’t recognize in an equation, it is almost certain to be a letter in the Greek alphabet, just look it up!
Okay, that’s all I have time for today. Hope this illuminated some basic math for people and if there is interest, next week we can get a little more in-depth.
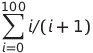

 YOUTUBE
YOUTUBE