Theory Behind FM Synthesis

In this tutorial we will look into how to predict and calculate the resulting sidebands in simple FM schemes, we will also look into Bessel functions, self-modulating oscillator and composite frequency modulation.

If you will be interested even further let me know and I will make tutorial on different operator algorithms and their basic use.

Vibrato can be considered the most basic form of frequency modulation. In this case a slow varying sub audio signal (from LFO) is used to modulate the frequency of the carrier resulting in slow variation of carrier pitch.

However if we use audio rate signal to modulate the frequency of the carrier much faster modulation of carrier’s frequency occur. Our ear cannot resolve this frequency changes any more instead we hear it as additional sidebands in the carrier sound. By additional sidebands I mean additional frequency partials or harmonics that are introduced into the carrier waveform.

Now this partials occur both sides of our fundamental frequency of the carrier. Why on both sides? Because the modulation signal in FM synthesis used to modulate the carrier frequency is bipolar which means the frequency of the carrier varies in both directions in the same way as with vibrato.

So the pitch goes up and down from that fundamental frequency of the carrier but again this happens in audio rate so we don’t hear this as a pitch fluctuation anymore but rather as additional harmonics or partials in our sound.

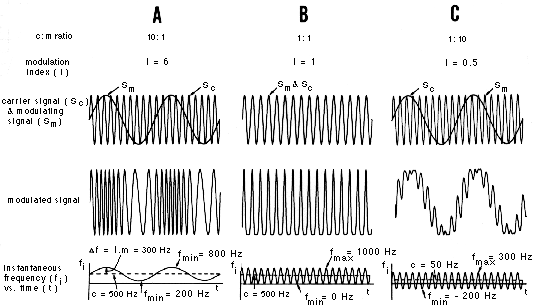
This deviation of the frequency of the carrier is proportional to the amplitude of the modulator. As we know the amplitude of modulator in FM synthesis is referred to as modulation amount or also modulation index.

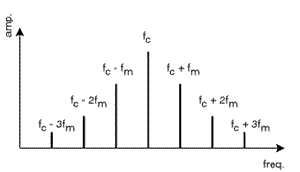
So the spectrum of the carrier sound is composed of the carrier frequency and a number of partials on either side of it and these are called sidebands. Even more, these partials around carrier frequency are spaced (in both directions) at a distance equal to the modulator frequency.

Calculating the frequencies of the partials

So let’s look into practical example:

We have a carrier and modulator set at simple integer ratio 4:1. So the frequency of the carrier is four times higher than frequency of the modulator. So let’s say we have a note playing at the frequency of 200Hz.

Now the frequency of our carrier will be 4*200Hz which equals 800Hz and the frequency of the modulator will be 200Hz because frequency ratio of C:M is 4:1.

Let’s see what happens to the carrier frequency if we modulate carrier at 800Hz with modulator set at 200Hz.

Numbers of partials occur around carrier frequency and that sidebands are integer multiples of the either carrier’s or modulator’s frequency (or both) resulting in richer harmonic spectra in the carrier waveform. Now the number of this generated sidebands depends on the modulation amount applied to the carrier.

We can calculate at which exact frequencies this sideband pairs occur and we must do that for both sum and difference sides of the sideband pair generated.

First let’s calculate sideband frequencies for positive deviation of the carrier frequency:

C=800Hz (Carrier frequency)

C+M=1000Hz (1st harmonic partial)

C+(2*M)= 1200Hz (2nd harmonic partial)

C+(3*M)=1400Hz (3rd harmonic partial)

C+(4*M)=1600Hz (4th harmonic partial)
and so on…

Now the negative deviation from the Carrier frequency:

C=800Hz (Carrier frequency)

C-M=600Hz (1st harmonic partial)

C-(2*M)=400Hz (2nd harmonic partial)

C-(3*M)=200Hz (3rd harmonic partial)
and so on…

As you can see all these sidebands frequencies are integer multiples of either carrier’s or modulator’s frequency.

This result in the highly harmonic spectrum of the sound.

Also note that when the lower sidebands extend below 0 Hz (like in the 4th harmonic partial case for the negative deviation) they are reflected back into frequency spectrum but in a 180 degree phase inverted form. By phase inverted I mean that the waveform flips over the x-axis, so negative parts of the sine wave become positive and vice versa.

Also when the partial in the upper end of the spectrum is beyond the Nyquist frequency (half the sampling rate) it folds over and reflects back to lower portion of the spectrum.

But when carrier and modulator are not in simple integer ratio relationship FM modulation generates inharmonic spectra in the carrier waveform which means sidebands are positioned on noninteger multiples of the carrier and modulator frequency.

So if we would have carrier set at 800Hz again but the modulator at 210Hz this time (ratio C:M is 8:2.1) the sidebands would be positioned in the frequency spectrum of the sound like this:

C=800Hz (Carrier frequency)

C+M=1010Hz (1st harmonic partial)

C+(2*M)= 1120Hz (2nd harmonic partial)

C+(3*M)=1230Hz (3rd harmonic partial)
and so on…

and for negative deviation:

C=800Hz (Carrier frequency)

C-M=590Hz (1st harmonic partial)

C-(2*M)=380Hz (2nd harmonic partial)

C-(3*M)=170Hz (3rd harmonic partial)
and so on…

As you can see and also hear this results in more dissonant type of a sound.

As we have seen we can predict the changes with most simple cases of FM synthesis where you have one sine wave modulator modulating the sine wave carrier at constant ratio and modulation values.

Frequency ratios and sound design

Here are few observations which are not like a set rules really but more like a guidelines:

• -If the ratio value of the carrier is equal to any integer and ratio of the modulator is equal to 1,2,3 or 4, then the resulting timbre will have a distinctive pitch, because the carrier frequency will always be prominent.
• -If the ratio value of the carrier is equal to any integer and ratio of the modulator is equal to any integer higher than 4, then the modulation produces harmonic partials but the fundamental may not be prominent.
• -If the ratio value of the carrier is equal to any integer and ratio of the modulator is equal to 1, then the modulation produces spectrum composed of harmonic partials. So the ratio of 1 : 1 would produce a sawtooth like wave.
• -If the ratio value of the carrier is equal to any integer and ratio of the modulator is equal to any even number, then the modulation produces a spectrum with some combination of odd harmonic partials. For example the ratio of C : M = 1 : 2 produces square like waveform.
• -If the ratio value of the carrier is equal to any integer and ratio of the modulator is equal to 3, then every third harmonic partial of the spectrum will be missing, e.g. the ratio of C : M = 1 : 3 produces narrow pulse like waves.
• -If the ratio value of the carrier is equal to any integer and ratio of the modulator is not equal to any integer then the modulation produces non-harmonic partials, so for instance C : M = 2 : 1.29 produces metallic bell like sound.

Bessel functions

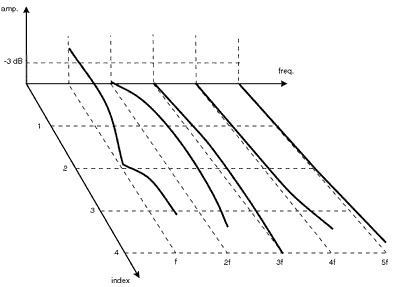
Another thing you should be aware of is when the ratio between modulator and carrier is constant and at fixed modulation amount the timbre of the sound will remain unchanged.

But when you vary the modulation amount of the modulators complex changes in the sound spectrum occur over time as the amplitudes of these partials in the sound changes.

These amplitude changes of each individual partial in the sound are determined by a class of mathematical functions called Bessel functions.

Each partial amplitude in the carrier waveform is determined by the slope of this Bessel function which are not linear in shape. So a specific partial may therefore increase or decrease its amplitude, according to a slope of it’s corresponding Bessel function at specific modulation values.

Here you can see how the amplitude of each partial is determined by it’s corresponding slope of the Bessel function in time. As you can see in the picture that linearly increasing the modulation index does not also necessarily increase the amplitude of the corresponding partial linearly.

Self-modulating Carrier

We should also look what happens if we modulate carrier by itself.

So in this case carrier output is used to modulate it’s own frequency. This will always produce sawtooth like wave due to the fact it works with a 1 : 1 frequency ratio by default, so the modulation frequency is equal to it’s own frequency.

Also the amplitudes of the partials increase proportionally to a modulation amount so more modulation you apply the brighter the sound gets, resulting in noise if the modulation index is very high.

The self-modulation technique is sometimes more preferable than the simple one carrier to one modulator (1 : 1) configuration since the amplitudes of the partials in this later case vary according to the Bessel functions and since this variation is not linear this results in more unnatural coloration of the signal.

The amplitudes of the partials produced by a self-modulating carrier increase more linearly according to the modulation amount so there is less of this unwanted coloration of the signal and for example this would be much more appropriate for something like simulation of a real instrument.

Composite Frequency Modulation

But where things get much more complex and interesting is when you use more than one modulator modulating more than one carrier, or one modulator two modulators which modulates two different carriers.

This we call Composite Frequency modulation. Here you can’t simply calculate the changes in the waveform anymore since these changes can be only described by using much more complex math very much beyond the scope of this tutorial but also beyond practical usage of FM synthesis for musical purposes.

These different configuration of carriers and modulators are reffered to as algorithms in FM8 (as in Yamaha DX7 synth).

There are quite a few different configurations of them such as additive carriers with independent modulators, additive carriers with one modulator, single carrier with parallel modulators, single carrier with serial modulators, self-modulating carriers and so on.

Here you can see some of these possible configurations:

With all these possibilities how to route operators possibilities are endless. And this is why with FM synthesis you can create very complex temporal evolution of the spectrum with complicated movement and tone variations which are not possible with other simpler forms of synthesis like subtractive synthesis for example.

Let me know if you are interested in this and I can make another tutorial on most common examples of algorithms in FM synthesis and their basic use.

Till then!